9.7. Arrays multi-dimensionais

Até agora usámos sempre arrays uni-dimensionais – vetores – mas também podemos declarar e criar arrays com duas ou mais dimensões.

Suponha que queremos representar, no nosso programa, a ocupação dos lugares de uma sala de cinema. Uma sala tem várias filas e cada fila tem vários lugares.

Podemos representar cada fila de lugares como um array de boolean, em que true e false significam, por exemplo, lugar ocupado e lugar livre, respetivamente. Podemos representar a sala de cinema como um array de elementos que representam filas de lugares.

Obtemos então um array de elementos que são, eles próprios, arrays.

Outro exemplo: queremos representar no nosso programa as notas que os alunos de uma turma obtiveram nas várias disciplinas do curso. Se pensarmos só nas notas que um único aluno obteve às várias disciplinas, concluímos que as podemos representar através de um array de inteiros. Como queremos representar as notas de vários alunos, podemos fazê-lo através de um array bi-dimensional: um array em que cada elemento representa as notas que um dado aluno obteve nas várias disciplinas, ou seja, um array de arrays de inteiros.

Como declaramos uma variável que representa um array bi-dimensional?

Exatamente da mesma forma que temos usado até aqui, declarando um array de elementos cujo tipo é, por sua vez, array. Dois exemplos:

x
boolean [] [] cinema;    // um array bi-dimensional de boolean
​
int [] [] notasAlunos;    // um array bi-dimensional de int

Como sabemos, estas declarações não criam os arrays. As variáveis ficam com valores indefinidos.

Tal como vimos para os vetores, podemos criar e inicializar os elementos de um array bi-dimensional de duas formas possíveis: com valores explícitos ou com os valores por defeito para o seu tipo.

xxxxxxxxxx
cinema =  { {true, false, true}, {true, false},
            {true, true, true, true}, {true, false}
           };
​
notasAlunos = new int [3] [5];

No primeiro caso, o nosso array tem 4 elementos, em que cada elemento é um array de boolean. Neste exemplo em particular, os elementos do array são arrays com tamanhos diversos pois estamos a representar a ocupação de uma sala de cinema em que a 1ª fila tem 3 lugares, e as restantes têm, respetivamente, 2, 4 e 2 lugares.

No segundo caso, o nosso array vai ter 3 elementos, em que cada elemento é um array com 5 inteiros. Todos esses 15 elementos inteiros ficam com um valor inicial de zero. Desta forma, todos os 3 arrays têm 5 elementos exatamente.

Quando todos os arrays elementos de um array bi-dimensional têm o mesmo número de valores, dizemos que o array bi-dimensional constitui uma matriz.

À semelhança das matrizes enquanto entidades matemáticas, aqui também distinguimos linhas e colunas numa matriz.

Na imagem seguinte representamos a variável notasAlunos, que contém uma referência a uma matriz com 3 linhas e 5 colunas, de uma forma que sugere bem a ideia de linhas e colunas. Na imagem, um array é representado por vários quadrados contíguos, tanto na vertical como na horizontal. Os números dentro dos quadrados representam os valores dos vários elementos dos arrays. O conteúdo de cada um dos quadrados à esquerda, na vertical, é uma seta pois representa uma referência a um objeto, neste caso uma referência a um array. O conteúdo de cada um dos elementos dos arrays na horizontal é um número, representando uma nota de um aluno. Os números a azul pretendem representar os índices das linhas (à esquerda, na vertical) e os índices de colunas (em cima, na horizontal).

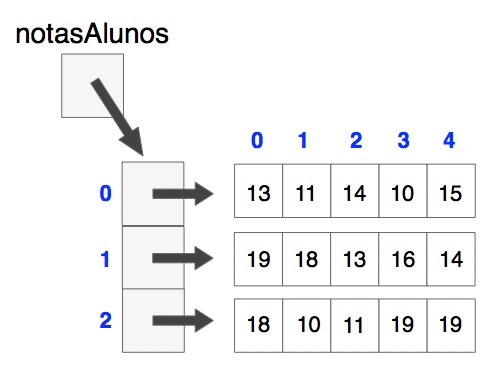
Podemos interpretar a matriz como representando as notas de 3 alunos em 5 disciplinas.

Cada linha da matriz representa as notas de um dado aluno nas 5 disciplinas. Por exemplo, a primeira linha representa um aluno que tem 13 na primeira disciplina, 11, 14, 10 e 15 nas seguintes, respetivamente.

Cada coluna da matriz representa as notas dos 3 alunos a uma dada disciplina. Por exemplo, na primeira disciplina, representada pela primeira coluna, os alunos tiveram 13, 19 e 18, respetivamente.

Repare que, neste exemplo:

• O valor da expressão notasAlunos.length é 3, pois o array referenciado pela variável notasAlunos tem 3 elementos;
• O valor da expressão notasAlunos[1].length é 5, pois o array referenciado pela variável notasAlunos[1] tem 5 elementos;
• De forma mais geral, o valor da expressão notasAlunos[i].length, para valores de i no intervalo [0, notasAlunos.length-1] é 5, pois cada um dos arrays referenciados pelas variáveis notasAlunos[0], notasAlunos[1] e notasAlunos[2] tem 5 elementos.

Como acedemos a um elemento de um array bi-dimensional? Através de dois índices, que representam a posição desse elemento na estrutura bi-dimensional representada pelo array. Por exemplo, cinema [3][1] tem o valor false e representa o 2º elemento pertencente ao 4º array do array bi-dimensional cinema.

No acesso a um elemento a[i][j] de um array bi-dimensional a, o valor de i tem que estar no intervalo [0, a.length-1] e o valor de j tem que estar no intervalo [0, a[i].length-1] .

Experimente executar o programa seguinte:

x
public class ArraysMultiDimensao {
   public static void main(String[] args){
      int [] [] notasAlunos = new int [3] [5];
      notasAlunos[2][0] = 18;
​
      boolean [] [] cinema =  { {true, false, true}, {true, false},
                                {true, true, true, true}, {true, false}
                               };
   }
}

Quais os valores iniciais dos elementos do array notasAlunos? Sim, são zero. Este é, como já sabe, o valor por defeito dado aos elementos do tipo int.

A figura abaixo pretende representar a memória no final da execução do programa. A forma de representar é semelhante à figura apresentada anteriormente. A diferença está somente na orientação dada aos vários arrays envolvidos.

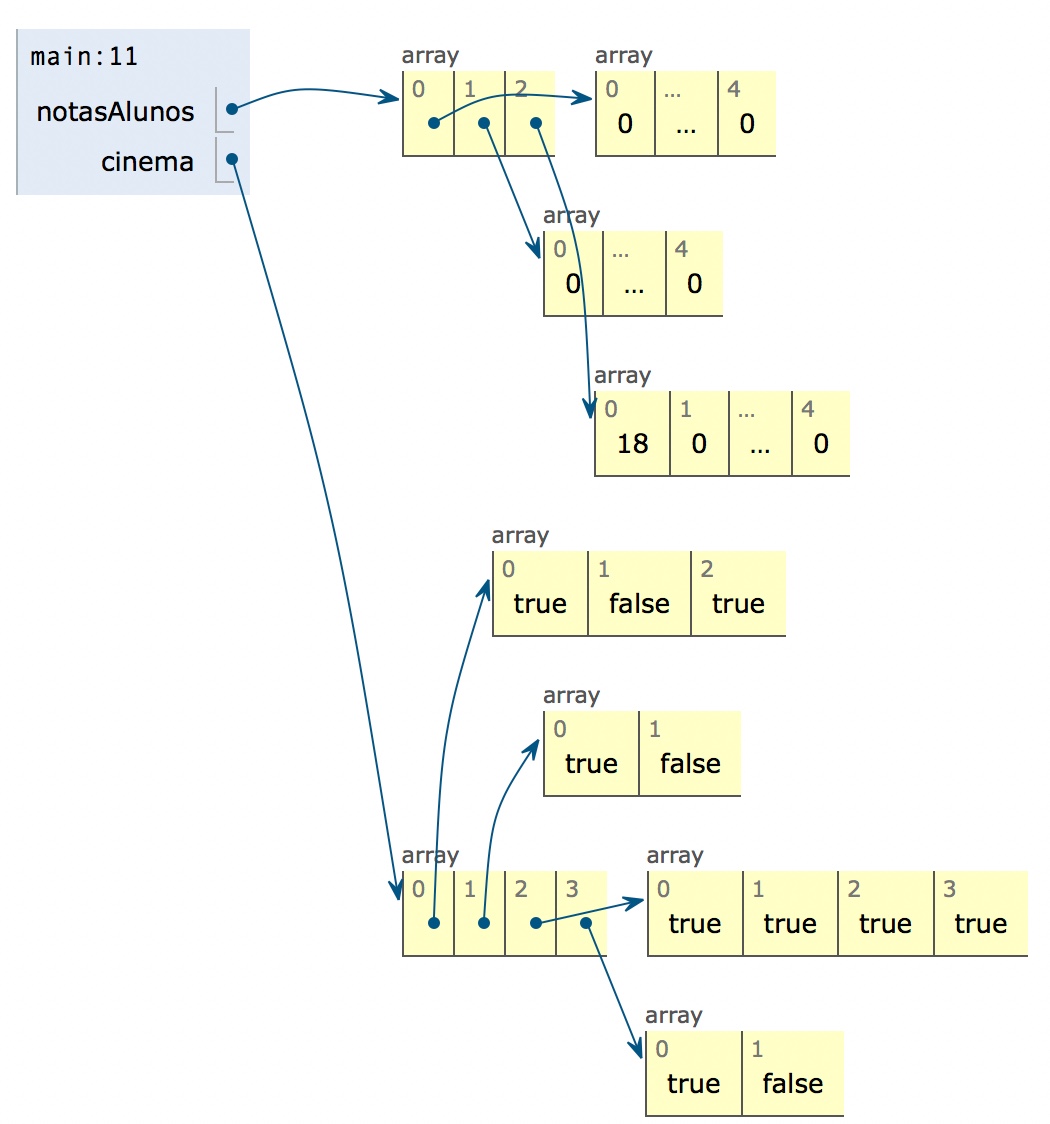
Pelo facto de cada linha de um array bi-dimensional ser um array, podemos usá-lo como tal. Por exemplo, o seguinte programa usa o segundo elemento de um array bi-dimensional para instanciar um parâmetro que está definido como um array uni-dimensional (vetor).

xxxxxxxxxx
public class ArraysMultiDimensao1 {
​
    public static void main(String[] args) {
        int [] [] m = { {5, -4, 11} , {33, 2, -1} };
        imprimeVetor(m[1]);
​
    }
    
    /**
     * Escrever os elementos de um vetor no standard output
     * @param a O vetor a escrever
     * @requires a != null
     */
    static void imprimeVetor(int[] a) {
        for(int i = 0 ; i < a.length ; i++) {
            System.out.print(a[i] + " ");
        }
        System.out.println();
    }
}

Cada m[i], para valores de i no intervalo [0, m.length - 1], é um vetor com 4 elementos.

Como podemos aceder a todos os elementos de um array bi-dimensional a para atuar de alguma forma sobre cada um deles?

Através de dois ciclos aninhados, com variáveis de progresso i e j, por exemplo, para permitir o acesso aos vários elementos a[i][j]. O ciclo externo é executado a.length vezes. O ciclo interno é executado, para cada valor de i, a[i].length vezes.

O método seguinte escreve os elementos de um array bi-dimensional a, de elementos do tipo int, no standard output.

x
static void imprimeArrayBi(int[][] a) {
    for(int i = 0 ; i < a.length ; i++) {
        for(int j = 0 ; j < a[i].length ; j++) {
            System.out.print(a[i][j] + " ");
        }
        System.out.println();
    }
}

Faz sentido ter arrays com mais que 2 dimensões? Claro, embora devamos ter cuidado para não criarmos estruturas tão complexas que se podem tornar difíceis de compreender e usar.

Se quisermos representar, num programa, as notas que os alunos de uma disciplina que tem várias turmas, com o mesmo número de alunos cada, tiveram aos vários testes feitos na disciplina, podemos usar um array tri-dimensional. Neste contexto, a instrução seguinte declara e inicializa a zero as notas que os alunos de uma disciplina que tem 3 turmas, com 28 alunos em cada turma, tiveram a cada um dos 4 testes.

xxxxxxxxxx
int[][][] notasTestes = new int[3][28][4];

O programa seguinte declara e cria um array tri-dimensional. De seguida atribui um valor específico a cada elemento. Estes valores são números pares sucessivos maiores ou iguais a -12. Experimente executá-lo.

x
public class ArraysMultiDimensao2 {
​
    public static void main(String[] args) {
        int [][][] multi = new int[2][3][4];
        int valor = -12;
        
        for(int i = 0 ; i < 2 ; i++) {
            for(int j = 0 ; j < 3 ; j++) {
                for(int k = 0 ; k < 4 ; k++) {
                    multi[i][j][k] = valor;
                    valor += 2;
                }
            }
        }
    }
}

Anterior: 9.6. Métodos com parâmetros do tipo array

Seguinte: 10. Criar novos tipos de dados