Cap6Sec6

6.6. A instrução `while`

No início da Secção 6.2., quando introduzimos o ciclo for, dissemos que a instrução for deve ser usada em qualquer situação em que o número de vezes que se quer repetir uma dada tarefa é limitado.

Se no programa TabelaDeTabuadas tivéssemos invocado o método imprimeTabuadas com dois valores dados pelo utilizador, por exemplo, não haveria maneira de nós, programadores, sabermos quais seriam esses valores na altura em que escrevêssemos o programa. Seriam potencialmente diferentes de cada vez que o programa fosse executado. E isto é muito bom!

No que diz respeito aos ciclos, o que nos interessa é que, quaisquer que fossem os valores dados pelo utilizador, eles seriam conhecidos na altura em que os ciclos fossem executados; então, na verdade o número de vezes que aqueles ciclos são executados é sempre limitado.

Existem casos, no entanto, em que não é conhecido nenhum limite máximo para o número de vezes que um ciclo tem de ser executado. Considere, por exemplo, o caso em que, dado um valor n, queremos descobrir o menor número primo que é maior que n.

Uma estratégia possível seria investigar, para cada número i a partir de n + 1, se i é primo e parar a pesquisa logo que o primeiro número primo fosse encontrado.

A questão aqui é que não é conhecido, à partida, o número máximo de vezes que o ciclo vai ser executado pois não se sabe quantos números, no máximo, vão ter que ser investigados (não é conhecido, em geral, qual o intervalo entre primos sucessivos).

Então, o número máximo de vezes que o ciclo é executado não é conhecido e não está, a priori, limitado. Nestes casos em que queremos exprimir repetição não limitada, usamos outra instrução de repetição – o ciclo while.

6.6.1. Sintaxe e semântica

A sintaxe geral do ciclo while pode ser descrita por:


while (guarda)
    corpo-do-ciclo

A guarda é uma expressão do tipo boolean (ou condição).

O corpo-do-ciclo é um bloco de instruções entre chavetas.

O fluxo de execução do ciclo while é representado pela seguinte figura.

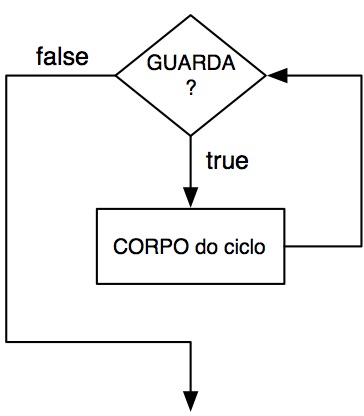
Um exemplo:


x
   /**
     * O menor primo maior que um dado numero
     * @param n - O numero
     * @requires n > 0
     * @return O menor primo maior que n
     */
   static int menorPrimoMaiorQue (int n) {
       int palpite = n + 1;
       while (menorDivisorMaiorQueUm(palpite) != palpite) {
           palpite++;
       }
       return palpite;
   }

Usamos o método menorDivisorMaiorQueUm, que fizemos na Secção 6.2.7, para testarmos se um número é primo – se a função, aplicada a um valor v, retorna o próprio v, é porque v é primo.

Vamos supor que a função menorPrimoMaiorQue é invocada com o valor 20 para o parâmetro n. A função começa por considerar o primeiro número maior que n, que é 21.

Esta primeira instrução funciona como que uma inicialização do ciclo pois a guarda depende do valor que a variável palpite vai tomando.

Acompanhando o fluxograma da figura da página anterior, vemos que a guarda é agora avaliada. Como a função menorDivisorMaiorQueUm aplicada a 21 dá 3, a guarda avalia para true. Segue-se a execução do corpo do ciclo, que incrementa a variável palpite para 22.

A guarda é de novo avaliada e de novo avalia para true. O corpo do ciclo é de novo executado e palpite fica com o valor 23.

Quando a guarda é de novo avaliada, o seu valor é false pois a função menorDivisorMaiorQueUm aplicada a 23 retorna 23, que não é diferente de 23. Então o ciclo termina e a função menorPrimoMaiorQue também, retornando o valor 23.

Esta função pode ser programada de forma mais eficiente. Tente encontrar passos desnecessários.

O corpo do ciclo deve mudar algo no estado do programa de modo a que a guarda, mais tarde ou mais cedo, se torne falsa e o ciclo termine. Se isso não acontecer temos um ciclo infinito.

Note que se a guarda é falsa logo à partida, o corpo do ciclo nunca chega a ser executado.

6.6.2. Mais exemplos

Se quisermos contar o número de algarismos de um dado inteiro, podemos dividi-lo por 10 (divisão inteira) sucessivamente obtendo, a cada divisão, um número com menos um algarismo. Se contarmos o número de vezes que conseguimos fazer isto, então ficamos a conhecer quantos algarismos tem o número original.

Seja n o número dado; queremos então repetir o seguinte bloco de instruções:


xxxxxxxxxx
   {
       n = n / 10;
       count++;
    }

Quantas vezes, no máximo, temos que repetir este bloco? Não sabemos ao certo quantas vezes, só sabemos que devemos repetir até não conseguirmos reduzir mais o número. Então vamos usar um ciclo while pois trata-se de repetição não limitada.

Qual a pergunta que temos que fazer para saber se ainda conseguimos reduzir o número? Se considerarmos somente valores de n não negativos, se n for maior ou igual a 10 ainda conseguimos diminuir-lhe um algarismo.


xxxxxxxxxx
    while (n >= 10) {
       n = n / 10;
       count++;
      }

Falta inicializar a variável count. Com que valor? Como o corpo do ciclo só é executado para valores maiores ou iguais a 10, devemos dar a count um valor inicial que represente o número de algarismos que os números menores que 10 têm. Devemos inicializá-la com o valor 1 pois todos os números não negativos menores que 10 têm um algarismo.


xxxxxxxxxx
    /**
     * O número de algarismos de um dado numero
     * @param n - O numero
     * @requires n >= 0
     * @return O numero de algarismos de n
     */
   static int quantosAlgarismos (int n) {
      int count = 1;
      while (n >= 10) {
         n = n / 10;
         count++;
      }
      return count;
   }

Quais os casos críticos que devemos analisar? Quando o parâmetro n:

é zero
está no intervalo ]0,10[
é 10

A forma como fomos construindo a solução desta função levou-nos a restringir a sua utilização. A pré-condição – condição descrita com a tag @requires – desta função diz-nos que só a devemos invocar para valores não negativos do seu parâmetro.

Se ignorarmos a pré-condição e invocarmos esta função com valores negativos obteremos resultados errados (exceto em algumas situações; sabe quais são?).

Se quisermos estender a utilização deste método a todos os valores negativos podemos trabalhar com o valor absoluto do parâmetro:


xxxxxxxxxx
/**
 * O número de algarismos de um dado numero
 * @param n - O numero
 * @return O numero de algarismos de n
 */
static int quantosAlgarismos (int n) {
      int count = 1;
      int num = Math.abs(n);
      while (num >= 10) {
         num = num / 10;
         count++;
      }
      return count;
}

Anterior: 6.5. Ainda o âmbito das variáveis

Seguinte: 6.7. A instrução do-while

6.6. A instrução while

6.6.1. Sintaxe e semântica

6.6.2. Mais exemplos

6.6. A instrução `while`